Функция в алгебре: её свойства, определение и понятие
 Одним из основных понятий в математике, если не самым основным, является понятие функции. Для понимания этого термина, его значения, смысла и необходимости, обратимся к следующему примеру:
Одним из основных понятий в математике, если не самым основным, является понятие функции. Для понимания этого термина, его значения, смысла и необходимости, обратимся к следующему примеру:
Вообразим себе обыкновенный автомобиль. Предположим, что он постоянно двигается со скоростью 80 км/ч и не меняет её на протяжении всего пути. А теперь попробуем выяснить: сколько километров проедет автомобиль, если в пути он будет находиться 5 часов? Итак, нам известна скорость и время. Попробуем составить зависимость:
Оглавление:
| Сколько времени находится в пути автомобиль? | Сколько километров автомобиль проехал? |
| 1 ч | 80 км |
| 2 ч | 160 км |
| 3 ч | 240 км |
| 4 часа | 320 км |
| 5 часов | 400 км |
 Нам были известны всего две величины: скорость автомобиля и время, которое он находился в пути. Взглянув на таблицу, можно понять, что между временем, которое находился автомобиль в пути, и пройденным им расстоянием есть чёткая зависимость — каждый час автомобиль проезжает на 80 километров больше. Что ж, давайте немного приблизимся к алгебре и введём две переменные: y и x.
Нам были известны всего две величины: скорость автомобиля и время, которое он находился в пути. Взглянув на таблицу, можно понять, что между временем, которое находился автомобиль в пути, и пройденным им расстоянием есть чёткая зависимость — каждый час автомобиль проезжает на 80 километров больше. Что ж, давайте немного приблизимся к алгебре и введём две переменные: y и x.
Y — это наше расстояние, а x — время пути. Составим уравнение: y = 80 * x. Теперь вместо x подставим время:
- Y = 80 * 1. Получается 80 — значение расстояния, которое автомобиль пройдёт за 1 час.
- Теперь вместо x подставим 2. Получается: y = 80 * 2 = 160. Это значение расстояния, которое пройдёт автомобиль при условии, что он будет ехать 2 часа.
Теперь введём следующую запись: y(x). Эта запись означает зависимость первой переменной от второй, а наше окончательное уравнение для движения автомобиля будет выглядеть следующим образом: y(x)=80x. Y в алгебре принято называть функцией, а x — аргументом.
Это интересно: какой вектор называется разностью двух векторов?
Смысл
 Пользуясь приведённым примером, мы чётко и ясно можем понять, что определение функции — это зависимость одной переменной от другой.
Пользуясь приведённым примером, мы чётко и ясно можем понять, что определение функции — это зависимость одной переменной от другой.
Очень важно понимать, что y = 80 * x — не единственная зависимость. Стоит нам лишь изменить скорость автомобиля, то все ý при тех же значениях аргумента будут совсем другие. Кроме того, существует огромное множество зависимостей, которые могут иметь другой вид.
Способы задания
Всего в математике существует три способа задания функции:
- «Формульный способ». С помощью формулы мы всегда можем определить ý. Допустим, что у нас есть зависимость y = 5x + 1. Чтобы найти все y, нам просто нужно подставить вместо x любое число, например: если x = 0, y = 1, если x = 5, y = 26. В этой функции мы можем принимать любые значения аргумента, но если нам встретится следующая зависимость: y = √x, то мы сможем взять за x все числа, кроме отрицательных, так как число под корнем не может быть с минусом.
- Табличный способ задания также очень сильно распространён. Мы уже встречались с таблицей, когда приводили пример про автомобиль. Для того чтобы составить таблицу, необходимо всего лишь найти несколько значений y при нескольких значениях аргумента.
- Графический способ задания. Когда только начинают знакомятся с функциями, обязательно вводят такое понятие, как график. Давайте рассмотрим, что же он из себя представляет.
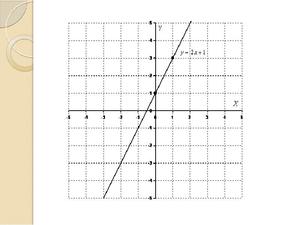
Перед вами координатная плоскость — основа для графика. Она состоит из вертикальной оси Y — оси значений, и из горизонтальной оси X — аргумента. У координатной плоскости обязательно есть начало отсчёта, которая обозначается нулём, и единичный отрезок (в данном примере единичный отрезок равен одной клетке).
На координатной плоскости мы можем взять любой единичный отрезок. Например, если нам удобно, значение одной клетки будет ни 1, а 100. Следовательно, две клетки — 200 и так далее. Здесь мы можем построить любой график и, соответственно, увидеть любую зависимость.
На координатной плоскости мы видим график 2x — 1. Графиком является прямая. Как же определить зависимость? Давайте приметим любое значение аргумента, например, 0. Когда x = 0, значение равно 1, что чётко видно на графике. Когда аргумент = -1, значение также равно -1.
Свойства
В алгебре есть невообразимое количество свойств функции, но основными и действительно важными являются лишь некоторые.
 «Область определения». Это понятие очень простое: оно подразумевает собой абсолютно все числа, которые может принимать переменная x. Например, в функции y = x — 2, переменная x может принимать все значения, то есть от минус бесконечности до плюс бесконечности. Другое дело, например, такая функция: y = √x. Так как под корнем не может стоять отрицательное число, допустимыми значениями аргумента могут быть все числа от нуля до плюс бесконечности.
«Область определения». Это понятие очень простое: оно подразумевает собой абсолютно все числа, которые может принимать переменная x. Например, в функции y = x — 2, переменная x может принимать все значения, то есть от минус бесконечности до плюс бесконечности. Другое дело, например, такая функция: y = √x. Так как под корнем не может стоять отрицательное число, допустимыми значениями аргумента могут быть все числа от нуля до плюс бесконечности.- Если область определения все значения аргумента, то следующее свойство функции, называемое «область значений» — это все значения, которые может принимать переменная y. Поскольку значения функции зависимы от аргумента, то тут ничего выдумывать не надо, а просто вычислять.
- «Ограниченность» определить очень просто: если в рассматриваемой функции существует максимальное или минимальное значение y, то мы говорим, что функция будет называться ограниченной либо сверху, либо снизу.
- «Непрерывность» —тоже очень простое свойство. Например, зависимость ý = 2x — 1, которую мы уже рассматривали, непрерывна, так как её график нигде не прерывается. Если же в какой-либо функции график будет прерываться, можно говорить, что она прерывается на определённом промежутке.
- «Выпуклость» также присуща не всем графикам. У линейной зависимости её быть не может, поскольку это прямая и она не может быть выпуклой. А, например, парабола может быть выпуклой либо вверх, либо вниз.
- Нули функции — это пересечение с осями. То есть, если нам необходимо описать данное свойство, нужно будет найти, в каком месте график пересекается с осью абсцисс и в каком месте с осью ординат.
Подводя итог, мы можем сказать, что функция — это важнейшее понятие в математике, ведь, по сути, ею можно описать любые процессы.
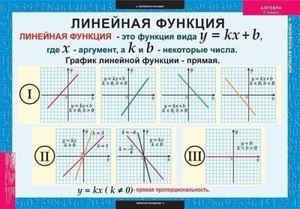 «Область определения». Это понятие очень простое: оно подразумевает собой абсолютно все числа, которые может принимать переменная x. Например, в функции y = x — 2, переменная x может принимать все значения, то есть от минус бесконечности до плюс бесконечности. Другое дело, например, такая функция: y = √x. Так как под корнем не может стоять отрицательное число, допустимыми значениями аргумента могут быть все числа от нуля до плюс бесконечности.
«Область определения». Это понятие очень простое: оно подразумевает собой абсолютно все числа, которые может принимать переменная x. Например, в функции y = x — 2, переменная x может принимать все значения, то есть от минус бесконечности до плюс бесконечности. Другое дело, например, такая функция: y = √x. Так как под корнем не может стоять отрицательное число, допустимыми значениями аргумента могут быть все числа от нуля до плюс бесконечности.



 2
2