Как перевести градусы в радианы: формулы перевода
 С давних времён люди измеряют углы. Но что такое угол? Геометрия даёт нам ответ: «Угол — это два луча, проведённые из заданной точки». Углы бывают разные: тупые, острые, прямые, развёрнутые, центральные, смежные. Возьмём точку O и проведём из неё луч O. A. Теперь из этой же точки проведём луч OB, параллельный лучу OA и направленный с ним в одну сторону. Про такие лучи говорят, что угол между ними составляет 0° (ноль градусов). Если мы теперь направим луч OB параллельно лучу OA, но в противоположную сторону, то получим развёрнутый угол, равный 180°.
С давних времён люди измеряют углы. Но что такое угол? Геометрия даёт нам ответ: «Угол — это два луча, проведённые из заданной точки». Углы бывают разные: тупые, острые, прямые, развёрнутые, центральные, смежные. Возьмём точку O и проведём из неё луч O. A. Теперь из этой же точки проведём луч OB, параллельный лучу OA и направленный с ним в одну сторону. Про такие лучи говорят, что угол между ними составляет 0° (ноль градусов). Если мы теперь направим луч OB параллельно лучу OA, но в противоположную сторону, то получим развёрнутый угол, равный 180°.
Оглавление:
Что означают градус и радиан
Так вот, мерой расхождения двух лучей, проведённых из одной точки друг от друга, будет градусное расстояние. Что такое градус? В переводе «градус» означает «шаг». Всего таких «шагов» может быть 360°. Это число было придумано ещё в глубокой древности математиками и астрономами, пользовавшимися шестидесятиричной системой счисления. Они брали круг, из центра которого проводили два радиуса. Мерой расхождения этих радиусов друг от друга был градус. Когда расстояние между радиусами в градусах отсчитывали против часовой стрелки, такой угол считался положительным, а когда против часовой — отрицательным.
Это интересно: умножение на 0 — правило для любого числа.
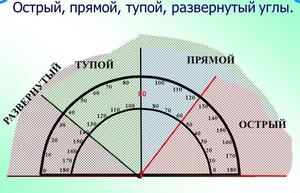 Вращая один радиус относительно другого против часовой стрелки, мы будем получать разные углы. Когда эти отрезки совпадают, то между ними будет 0°, когда же отрезки отсекают сектор круга, равный одной четверти полного круга, то угол между ними составит 90°. Вращая дальше таким образом, мы получим следующие углы: 180° — радиусы лежат на диаметре круга и делят его пополам, 270° — радиусы отсекают три четверти круга, 360° — радиусы совпадают. Таким образом, полный круг составляет 360°. Для измерения углов существует транспортир.
Вращая один радиус относительно другого против часовой стрелки, мы будем получать разные углы. Когда эти отрезки совпадают, то между ними будет 0°, когда же отрезки отсекают сектор круга, равный одной четверти полного круга, то угол между ними составит 90°. Вращая дальше таким образом, мы получим следующие углы: 180° — радиусы лежат на диаметре круга и делят его пополам, 270° — радиусы отсекают три четверти круга, 360° — радиусы совпадают. Таким образом, полный круг составляет 360°. Для измерения углов существует транспортир.
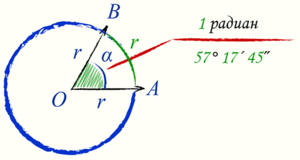 Кроме градусной меры для измерения углов применяют меру радианную. Радиан — это мера центрального угла. «Радиан» означает «связанный с радиусом». Если из центра окружности радиусом R провести два луча, то они на ней отсекут дугу, длина которой l. Так вот, угол α между указанными лучами называется центральным. Чтобы его измерить, нужно длину дуги окружности разделить на её радиус: α=l/R. Получится значение, выраженное в радианах (рад). Поскольку любому углу на плоскости можно сопоставить такой же центральный угол, то встаёт вопрос, как от обычной градусной меры перейти к радианной.
Кроме градусной меры для измерения углов применяют меру радианную. Радиан — это мера центрального угла. «Радиан» означает «связанный с радиусом». Если из центра окружности радиусом R провести два луча, то они на ней отсекут дугу, длина которой l. Так вот, угол α между указанными лучами называется центральным. Чтобы его измерить, нужно длину дуги окружности разделить на её радиус: α=l/R. Получится значение, выраженное в радианах (рад). Поскольку любому углу на плоскости можно сопоставить такой же центральный угол, то встаёт вопрос, как от обычной градусной меры перейти к радианной.
Это интересно: признак перпендикулярности прямой и плоскости, теория и практика.
Как перевести градусы в радианы и обратно
Мы знаем, что центральному углу в 360° соответствует вся окружность, длина которой вычисляется по известной формуле l=2•π•R. Разделим это выражение на R и получим: α= 2•π•R/R=2•π рад≈6,28 рад. Если взять какое-то угловое расстояние в A град., то его радианная мера α получится из пропорции: А/360°=α/(2•π). Решив это уравнение, получим формулу перевода градусов в радианы — α=(π/180°)•А, или формулу перевода радиан в градусы — А=(180°/π)•α. Из этих формул мы придём к следующим соотношениям:
- 1 рад=180°/π≈57,2958°;
- 1°=π/180 рад≈0,01745 рад.
Сколько составит 180 градусов в радианах и 90 градусов в радианах? Воспользовавшись полученными выше формулами, придём к таким соотношениям:
- 90°=π/2 рад≈1,571 рад;
- 180°=π рад≈3,142 рад.
Итак, как правильно переводить градусную меру в радианную и обратно? В этом вам поможет следующее правило:
Чтобы найти число радиан, нужно градусную меру умножить на число π и поделить на 180. Чтобы найти число градусов, нужно радианную меру умножить на 180 и поделить на число π.
Примеры решения задач
Задача 1. Чему равна длина дуги окружности, если R=1 см, α=1 рад?
Решение. По формуле длины дуги найдём: l=R•α=1•1=1 см.
Задача 2. Сколько рад в 45°?
Решение. Используя правило, получим: α=45•π/180=π/4 рад.
Задача 3. Сколько град. в π² рад?
Решение. Используя правило, найдём: А=π²•180/π=180π град.≈565,5°.
Задача 4. Чему равен средний угловой размер лунного диска, если среднее расстояние до Луны равно R=384399 км, а диаметр самой Луны D=3476 км?
Решение. Если мысленно на Луну с Земли провести два луча, которые пройдут через крайние точки диаметра её диска, мы получим центральный угол, исходящий из глаз наблюдателя. Поскольку расстояние до Луны намного превышает её диаметр, то этот диаметр можно будет приравнять длине дуги l окружности, образуемой радиусом R, т. е. D≈l=α•R. Тогда искомый угловой размер составит: α≈D/R=3476/384399=0,00904268742 рад=0,51810782462°≈31’05»≈0,5°. Итак, видимый угловой диаметр Луны равен полградуса.
Это интересно: что такое разность в математике?
Минуты и секунды
 Издревле для измерения углов пользовались так называемой шестидесятиричной системой исчисления. В этой системе вся окружность делится на 360°. Затем каждый градус делят на 60 минут, а каждую минуту — на 60 секунд. Минуты обозначаются значком «'», а секунды — значком «». Отсюда пошло измерение времени. Кроме того, циферблат — это символ круга, а стрелки часов отмеряют центральные углы. Для перевода этих единиц используйте следующие соотношения:
Издревле для измерения углов пользовались так называемой шестидесятиричной системой исчисления. В этой системе вся окружность делится на 360°. Затем каждый градус делят на 60 минут, а каждую минуту — на 60 секунд. Минуты обозначаются значком «'», а секунды — значком «». Отсюда пошло измерение времени. Кроме того, циферблат — это символ круга, а стрелки часов отмеряют центральные углы. Для перевода этих единиц используйте следующие соотношения:
- 1°=60’=3600»;
- 1’=(1/60)°=60»;
- 1»=(1/3600)°=(1/60)’;
- 1 рад≈3438′. Приставочный способ вы найдете ответ по ссылке.





 1
1