Сформулируйте и докажите утверждения о признаках параллелограмма
Параллелограммом называют четырёхугольник (фигура, что состоит из четырёх точек и отрезков, последовательно их соединяющих), у которого противоположные стороны попарно параллельны. Его свойства впервые детально изучали греческие математики Евклид и Пифагор. Конец эпохи Средневековья принёс людям полную теорию об этой фигуре.
Оглавление:
История возникновения термина
О некоторых видах четырёхугольников, квадратов, прямоугольников, равносторонних и прямоугольных трапеций знали ещё давно. Первые найденные работы принадлежат египетским и вавилонским математикам.
Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.
Термин «параллелограмм» греческого происхождения, считают что его придумал Евклид (приблизительно 300 годов до нашей эры). Ещё известно, что эта фигура и её свойства были знакомы ученикам школы Пифагора, раньше их называли пифагорейцами.
В «Началах» Евклида приведена следующая теорема: в параллелограмме противоположные стороны равны, а диагонали разделяют его по половине. Но в данной книге не было написано о свойствах точки их сечения. Ещё этот учёный не упоминает о прямоугольнике и ромбе.
Это интересно: в геометрии луч — это что такое, основное понятие.
Полную теорию сделали только в конце Средневековья, а в книгах она появилась в семнадцатом столетии. Теоремы и свойства параллелограмма основывались на аксиомах Евклида.
«Диагональ» — это слово греческого происхождения, «диа» означало «через», а «гониос» — «угол». Это можно понять как отрезок, что соединяет вершины углов.
Нужно сказать, что Евклид, как и большинство математиков того времени, для названия отрезка, который соединяет противоположные вершины четырёхугольника или прямоугольника, использовал другой термин — «диаметр». Это можно объяснить тем, что первые геометры свои мысли основывали на вписании круга в прямоугольник. В Средние века для названия приведённых отрезков использовали оба термина. Только в семнадцатом столетии «диагональ» стала общепринятой.
Это интересно: разность векторов, определение разности.
Доказательство признаков фигуры
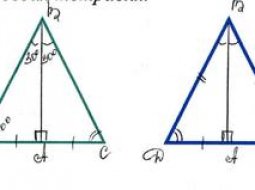
На следующем рисунке изображён параллелограмм ABCD, где AB параллельно CD и AD параллельно BC:
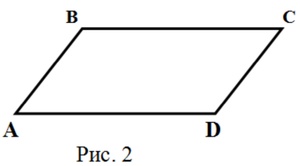
Сумма любых двух соседних углов параллелограмма равна 180 градусам — это первая подсказка о том, как сформулировать и доказать утверждения о признаках параллелограмма.
На этом рисунке углы A и B фигуры ABCD есть внутренними односторонними углами для параллельных прямых AD и BC . Поэтому углы A + B равны 180 градусам. Аналогично это свойство можно привести для любой другой пары соседних (если вершины есть концами одной и той же стороны) углов.
Нужно знать! Что такое горизонталь и горизонтальное положение.
Теорема признаков паралелограмма
- Теорема признаков параллелограмма гласит, что это выпуклый четырёхугольник. Исходя из предыдущего правила, угол А намного меньше 180 градусов, как и B, C, D, поэтому его называют опухлым четырёхугольником. Диагонали этой фигуры могут пересекаться.
- У параллелограмма противоположные стороны и углы равны.
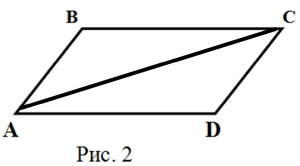Диагональ АС разбивает фигуру на два треугольника ABC и ADC. АС — общая сторона двоих треугольников и САD эквивалентен АСВ также с САВ и АСD. Тогда ∆АВС = ∆СDA, по стороне и двумя прилегающими углами. Это значит, что АВ=СD, BC=AD и B=D, как соответствующие элементы в различных треугольниках. В результате угол BAC + CAD равен ВСА + DCA и BAD = BCD.
Теорема о диагоналях
- Периметр (сумма длин всех сторон четырёхугольника, которую обозначают буквой Р) параллелограмма эквивалентен 2 (АВ +ВС) или АВ + ВС + СD + DA.
- Теорема о диагоналях параллелограмма гласит, что точкой пересечения они делятся ровно пополовине.
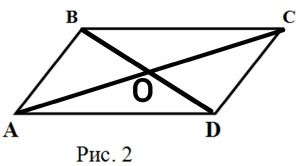По условию задачи O — это точка пересечения диагоналей AC и BD параллелограмма. AB эквивалентно BC, как противоположные, не имеющие своей общей вершины. CAD равен ACB также BDA и DBC, АD и BC секущими AC и B. D. Следуя дальше ∆АОD = ∆ COB, по стороне и двух прилегающих углах. Тогда, А = ОС, ВО = ОD, как соответствующие стороны разных треугольников.
Высотой называется перпендикуляр, проведённый из любой точки стороны фигуры к прямой, что имеет противоположную сторону.
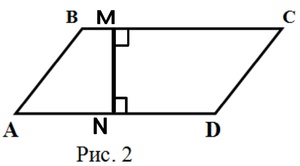На этом рисунке MN — это высота. Следуя за известным определением, из каждой вершины можно провести две высоты (BF и BT, которые приведены в соответствии к сторонам AD и CD).
Свойства параллелограмма с доказательствами 8 класса :
- Две стороны равны и параллельны.
- Противоположные стороны попарно равны.
- Диагонали пересекаются и этой точкой делятся ровно пополам.
- Противоположные углы попарно равны.
Теперь нужно вернуться к первому рисунку, чтобы до конца понять все признаки параллелограмма и доказательства любых признаков.
В нём AD = BC и AD || BC. Провели диагональ AC и получили ∆CAD и ∆ACB. CAD эквивалентен ВСА, как внутренние разносторонние углы при пересечениях прямых AD и BC секущей AC, ещё она является их общей стороной. Условия задачи говорят: AD=BC. Значит, что, ∆CAD=∆ACB, ACD = CAB. Из-за того, что они были созданы в таких условиях AB || CD, по признаку параллельных прямых.
